Дистанционно-векторный алгоритм и обратная коррекция

Обсуждавшегося выше сценария со счетом до бесконечности (см. рис. 4.9) можно избежать, если использовать метод, называемый обратной коррекцией, или «отравлением» обратного пути (poisoned reverse). Идея этого метода проста — если узел Z направляет пакеты узлу X через узел У, тогда узел Z объявит узлу Y, что его (узла Z) расстояние до узла X равно бесконечности. Узел Z будет продолжать говорить узлу Y эту «маленькую ложь» до тех пор, пока узел Z направляет пакеты узлу X через узел Y. Поскольку узел Y полагает, что у узла Z нет пути к узлу X, узел Уникогда не станет пытаться посылать пакеты узлу X через узел Z, пока узел Z продолжает посылать пакеты узлу X через узел Y (и лгать о том, что у него нет пути к узлу X).

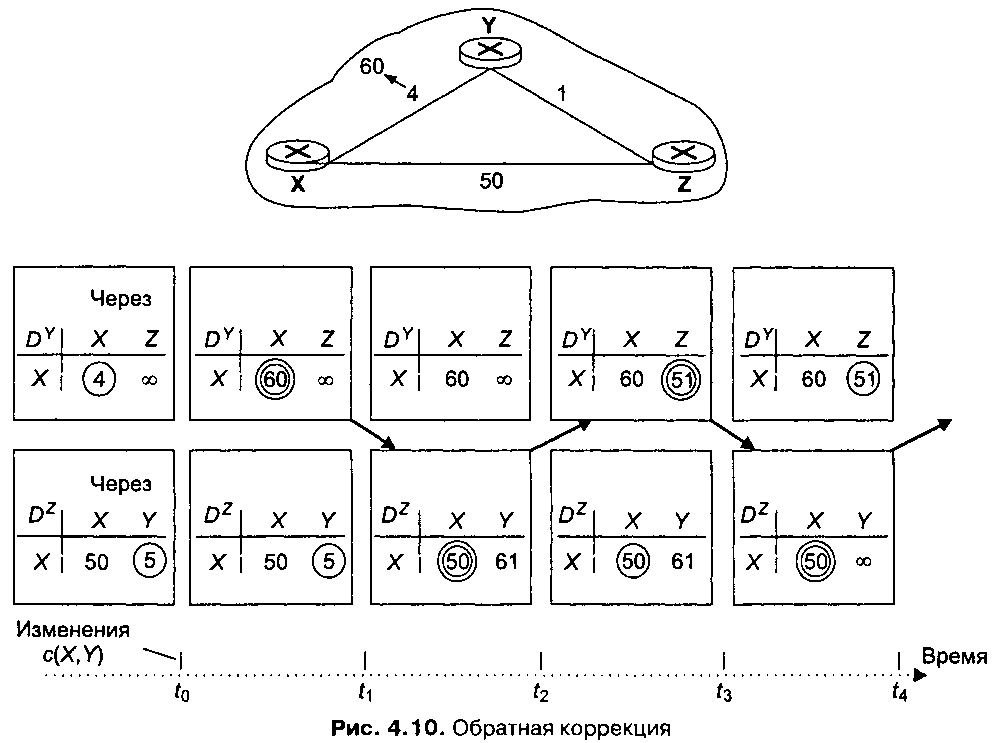
На рис. 4.10 показано, как метод обратной коррекции решает проблему маршрутных петель, с которой мы столкнулись на рис. 4.9. В результате обратной коррекции в таблице расстояний узла Y в записи стоимости пути до узла X через узел Z указана бесконечность (так как узел Z сообщил узлу Y, что расстояние от узла Z до узла X равно бесконечности). Когда в момент времени t0 стоимость линии XY увеличивается с 4 до 60, узел У обновляет свою таблицу, но продолжает направлять пакеты узлу X напрямую, несмотря на увеличившуюся стоимость маршрута, а также информирует узел Z об изменении стоимости. Получив это извещение в момент времени tu узел Z немедленно изменяет свой маршрут к узлу X на прямую линию ZX стоимости 50. Поскольку маршрут к узлу X изменился, и этот новый маршрут более не проходит через узел F, узел Z сообщает узлу Y о своем новом маршруте в момент времени t2. Получив эту информацию, узел Y обновляет свою таблицу расстояний, изменяя свой маршрут к узлу X. Теперь этот маршрут стоимости 51 проходит через узел Z. Кроме того, поскольку через узел Z теперь проходит путь наименьшей стоимости от узла Fk узлу X, узел Y «отравляет» обратный путь от узла Z до узла X, сообщая в момент времени t3 узлу Z, что стоимость пути от узла 7до узла X равна бесконечности. Этот алгоритм успокаивается в момент времени £4, со значениями таблицы расстояний для адресата Х1 показанными в правом столбце.

Позволяет ли метод «отравления» обратного пути решить проблему счета до бесконечности в общем случае? Нет. Вы можете убедиться сами, что петли, состоящие из трех и более узлов (а не просто из двух смежных узлов, какие мы видели на рис. 4.10), метод обратной коррекции распознать не сможет.